二つのさいころ と
と があり,各面に
があり,各面に ,
, ,
, ,
, ,
, ,
, という目が書かれている.
という目が書かれている.
これらのさいころについて, のさいころの各面には
のさいころの各面には ,
, ,
, ,
, ,
, ,
, の目のシールを
の目のシールを
貼り, のさいころの各面には
のさいころの各面には ,
, ,
, ,
, ,
, ,
, の目のシールを貼った.
の目のシールを貼った.
はじめに硬貨を投げ,次に と
と のさいころを同時に投げる次の試行を行う.
のさいころを同時に投げる次の試行を行う.
●硬貨を投げて表が出れば,両方のさいころのシールをすべてはがして二つのさいころ
を同時に投げる.
●硬貨を投げて裏が出れば,両方ともシールをはがさずに二つのさいころを同時に投げる
この試行について次の問いに答えよ.ただし,シールの有無にかかわらず,さいころの
各面の出方は同様に確からしいとする.
 二つのさいころの目の和が
二つのさいころの目の和が の倍数になる場合は,硬貨を投げて表が出たとき
の倍数になる場合は,硬貨を投げて表が出たとき

 通りあり,裏が出たとき
通りあり,裏が出たとき
 通りある.したがって,この試行において
通りある.したがって,この試行において
二つのさいころの目の和が の倍数になる確率は
の倍数になる確率は
 である.
である.
また,目の和が の倍数であるという条件のもとで,二つのさいころの目の差が
の倍数であるという条件のもとで,二つのさいころの目の差が 以下で
以下で
ある条件つき確率は
 である.
である.
 この試行における二つのさいころの目の和を表す確率変数を
この試行における二つのさいころの目の和を表す確率変数を とする.
とする.
硬貨を投げて表が出たとき,同時に投げた二つのさいころの目の和の平均 期待値
期待値 は
は

 であり,その分散は
であり,その分散は
 である.
である.
硬貨を投げて裏が出たとき,同時に投げた二つのさいころの目の和の平均は

 であり,その分散は
であり,その分散は
 である.
である.
したがって,この試行における の平均
の平均 は
は
 であり,分散
であり,分散 は
は

である.

 二つのさいころの目の和が
二つのさいころの目の和が の倍数になる場合は,硬貨を投げて表が出たとき
の倍数になる場合は,硬貨を投げて表が出たとき
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, の
の
 通り.硬貨を投げて裏が出たときも,
通り.硬貨を投げて裏が出たときも,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, の
の
 通りある.
通りある.
したがって,この試行において二つのさいころの目の和が の倍数になる確率は,
の倍数になる確率は,
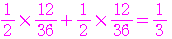
 となる.
となる.
また,目の和が の倍数であるという条件のもとで,二つのさいころの目の差が
の倍数であるという条件のもとで,二つのさいころの目の差が 以下
以下
となるのは,上記の 通りのうち,該当するのは,
通りのうち,該当するのは,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, の
の 通りだから,求める条件つき確率は,
通りだから,求める条件つき確率は,
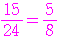
 となる.
となる.

 硬貨を投げて表が出たとき,同時に投げた二つのさいころの目の和
硬貨を投げて表が出たとき,同時に投げた二つのさいころの目の和 の確率分布
の確率分布
は,以下のようになる.

よって,求める平均 期待値
期待値 は
は
 +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+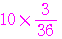
+ +
+ =
= =
=
また,その分散は,
 +
+ +
+ +
+ +
+ +
+ +
+ +
+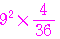
+ +
+ +
+ =
= =
=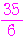
 硬貨を投げて裏が出たとき,同時に投げた二つのさいころの目の和
硬貨を投げて裏が出たとき,同時に投げた二つのさいころの目の和 の確率分布
の確率分布
も,上記と全く同じで以下のようになる.

よって,求める平均は ,その分散は
,その分散は
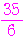
 となる.
となる.
したがって,この試行における の平均
の平均 は,
は,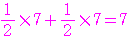
 であり,
であり,
分散 は,
は,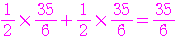
 となる.
となる.
 と
と があり,各面に
があり,各面に ,
, ,
, ,
, ,
, ,
, という目が書かれている.
という目が書かれている. のさいころの各面には
のさいころの各面には ,
, ,
, ,
, ,
, ,
, の目のシールを
の目のシールを のさいころの各面には
のさいころの各面には ,
, ,
, ,
, ,
, ,
, の目のシールを貼った.
の目のシールを貼った. と
と のさいころを同時に投げる次の試行を行う.
のさいころを同時に投げる次の試行を行う. 二つのさいころの目の和が
二つのさいころの目の和が の倍数になる場合は,硬貨を投げて表が出たとき
の倍数になる場合は,硬貨を投げて表が出たとき
 通りあり,裏が出たとき
通りあり,裏が出たとき
 通りある.したがって,この試行において
通りある.したがって,この試行において の倍数になる確率は
の倍数になる確率は
 である.
である. の倍数であるという条件のもとで,二つのさいころの目の差が
の倍数であるという条件のもとで,二つのさいころの目の差が 以下で
以下で
 である.
である. この試行における二つのさいころの目の和を表す確率変数を
この試行における二つのさいころの目の和を表す確率変数を とする.
とする. 期待値
期待値 は
は
 であり,その分散は
であり,その分散は
 である.
である.
 であり,その分散は
であり,その分散は
 である.
である. の平均
の平均 は
は
 であり,分散
であり,分散 は
は


 二つのさいころの目の和が
二つのさいころの目の和が の倍数になる場合は,硬貨を投げて表が出たとき
の倍数になる場合は,硬貨を投げて表が出たとき ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, の
の 通り.硬貨を投げて裏が出たときも,
通り.硬貨を投げて裏が出たときも, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, の
の 通りある.
通りある. の倍数になる確率は,
の倍数になる確率は,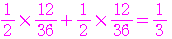
 となる.
となる. の倍数であるという条件のもとで,二つのさいころの目の差が
の倍数であるという条件のもとで,二つのさいころの目の差が 以下
以下 通りのうち,該当するのは,
通りのうち,該当するのは, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, の
の 通りだから,求める条件つき確率は,
通りだから,求める条件つき確率は,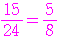
 となる.
となる.
 硬貨を投げて表が出たとき,同時に投げた二つのさいころの目の和
硬貨を投げて表が出たとき,同時に投げた二つのさいころの目の和 の確率分布
の確率分布
 期待値
期待値 は
は
 +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+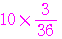
 +
+ =
= =
=
 +
+ +
+ +
+ +
+ +
+ +
+ +
+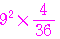
 +
+ +
+ =
= =
=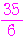
 硬貨を投げて裏が出たとき,同時に投げた二つのさいころの目の和
硬貨を投げて裏が出たとき,同時に投げた二つのさいころの目の和 の確率分布
の確率分布
 ,その分散は
,その分散は
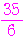
 となる.
となる. の平均
の平均 は,
は,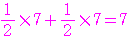
 であり,
であり, は,
は,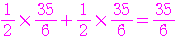
 となる.
となる.