に内接する三角形
に内接する三角形 があり,
があり, =
= ,
, =
= ,
, =
= である.
である.
 ,
,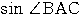
 の値を求めよ.
の値を求めよ. 円
円 の半径および三角形
の半径および三角形 の面積を求めよ.
の面積を求めよ. 点
点 を通る円
を通る円 の直径
の直径 を引き,直線
を引き,直線 との交点を
との交点を とする.このとき,
とする.このとき, の長さを求めよ.また,比
の長さを求めよ.また,比 :
: を最も簡単な整数の比で表せ.
を最も簡単な整数の比で表せ.

 これより,
これより, =
= =
=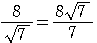
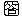
 の面積を
の面積を とすると,
とすると,
 =
= =
= =
=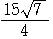
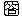

 は直径だから,
は直径だから, =
= =
= ,
, =
= したがって,
したがって, =
= =
= =
= =
=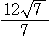
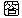
 と△
と△ は点
は点 からの高さが共通だから,面積の比は底辺の比の
からの高さが共通だから,面積の比は底辺の比の :
: に等しい.いま,
に等しい.いま, =
= とおくと,
とおくと, =
= −
− となるから,
となるから, =
= =
=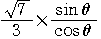
 =
= よって,
よって, :
: =
= :
: