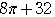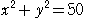
 …①
…① と直線
と直線
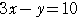
 の交点を
の交点を ,
, とする.ただし,点
とする.ただし,点 の
の
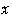
 座標は
座標は の
の
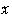
 座標より大きいものとする.
座標より大きいものとする. 点
点 ,
, の座標を求めよ.
の座標を求めよ. 線分
線分 上の点
上の点 を中心とする半径
を中心とする半径
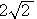
 の円の周を
の円の周を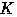
 とする.また,円①の周
とする.また,円①の周 とする.
とする.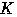
 が
が に含まれるとき,点
に含まれるとき,点 の
の
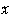
 座標
座標
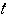
 のとりうる値の範囲を
のとりうる値の範囲を
 の点
の点 の
の
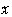
 座標
座標
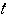
 が
が で求めた範囲を動くとき,
で求めた範囲を動くとき,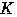
 が通過する領域を
が通過する領域を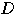
 とする.
とする.
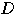
 の面積を求めよ.
の面積を求めよ.

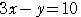
 …②とする.①,②から
…②とする.①,②から
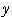
 を消去して,
を消去して, 整理して,
整理して,
 ,
,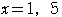
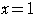
 のとき,②より,
のとき,②より, ,
,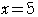
 のとき,②より,
のとき,②より,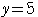
 の
の
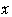
 座標は点
座標は点 の
の
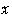
 座標より大きいので,
座標より大きいので, ,
, ,
, ,-
,-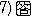
 円①の中心は原点,半径は
円①の中心は原点,半径は であるから,点
であるから,点 を中心とする半径
を中心とする半径 の円の
の円の が
が に含まれるための条件は,
に含まれるための条件は,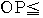
 -
- =
=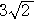
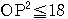
 …③ ここで,点
…③ ここで,点 の座標は,
の座標は,
 ,
,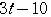
 ただし,
ただし,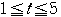
 と
と
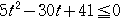
 これは,
これは,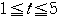
 を満たす.
を満たす.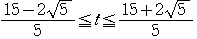
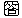

 より,
より, ,
,
 として,
として, ,
,
 のときの点
のときの点 を,
を, ,
,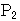
 とすると,
とすると,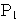

 ,
,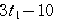
 ,
,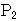

 ,
,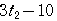
 より,線分
より,線分 の長さは
の長さは =
= =
= =
= =
=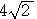
 線分
線分 の長さは
の長さは の直径に等しいから,
の直径に等しいから,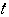
 が
が で求めた範囲を動くとき,
で求めた範囲を動くとき, が通過する領域
が通過する領域 は右図の斜線部分である.
は右図の斜線部分である.
 およびその内部の面積
およびその内部の面積 +
+
 の直径
の直径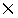
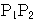
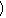
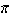
 +
+ =
=