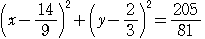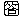,
, ,
, ,
, ,
, ,
,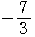
 がある.線分
がある.線分 を
を :
: に内分する点を
に内分する点を とし,直線
とし,直線 を
を
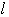
 とする.
とする. 点
点 の座標を求めよ.また,直線
の座標を求めよ.また,直線
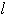
 の方程式を求めよ.
の方程式を求めよ. 2点
2点 ,
, を通る円
を通る円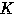
 の中心の
の中心の
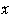
 座標を
座標を
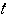
 とする.円
とする.円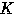
 の半径を
の半径を
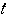
 の式で表せ.
の式で表せ. 直線
直線
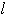
 と
と の円
の円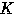
 との交点を
との交点を ,
, とする.線分
とする.線分 の長さが最小となるときの
の長さが最小となるときの
 の方程式を求めよ.
の方程式を求めよ.

 =
= :
: だから,点
だから,点 の座標は,
の座標は, =
=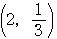

 直線
直線
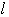
 の方程式は,
の方程式は,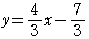
 円
円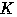
 の中心を
の中心を とすると,点
とすると,点 は線分
は線分 の
の の中点の座標は,
の中点の座標は, また,線分
また,線分 の傾きは,
の傾きは, だから,
だから, である.したがって,
である.したがって, つまり,
つまり, よって,点
よって,点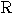
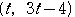
 とおけるから,
とおけるから,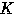
 の半径は,
の半径は, =
= =
= =
=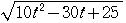

 円
円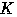
 の中心
の中心 から直線
から直線
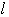
 に垂線をおろした足を
に垂線をおろした足を とすると,
とすると, は弦
は弦 の中点となるから,
の中点となるから, =
=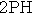
 が最小のとき,
が最小のとき, も最小となる.
も最小となる.
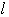
 の方程式は,
の方程式は,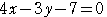
 と変形できるので,
と変形できるので, は,点
は,点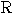
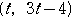
 と直線
と直線
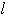
 との距離であるから,
との距離であるから, =
= =
= =
=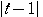
 =
= −
− =
= −
− =
=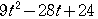
 となり,
となり,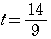
 のとき,
のとき,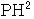
 は最小となる.したがって,
は最小となる.したがって, も最小となり,線分
も最小となり,線分 の長さも最小となる.点
の長さも最小となる.点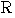
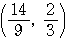
 だから,
だから, =
= =
= =
= よって,求める円
よって,求める円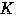
 の方程式は,
の方程式は,