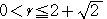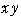
 平面上に4点
平面上に4点 ,
, ,
, ,
, ,
, -
- ,
, ,
, ,-
,- がある.正方形
がある.正方形 の
の
内部と周をあわせた領域を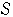
 とする.
とする.
 点
点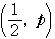
 が領域
が領域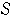
 に属するとき,
に属するとき,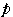
 のとりうる値の範囲を求めよ.
のとりうる値の範囲を求めよ.
 円
円
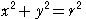
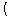
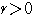
 と正方形
と正方形 の辺および頂点が共有点をもつとき,
の辺および頂点が共有点をもつとき,
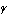
 のとりうる値の範囲を求めよ.
のとりうる値の範囲を求めよ.
 不等式
不等式
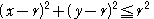
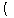
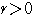
 の表す領域を
の表す領域を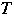
 とする.領域
とする.領域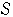
 と領域
と領域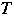
 が
が
共有点をもつとき,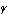
 のとりうる値の範囲を求めよ.
のとりうる値の範囲を求めよ.


 領域
領域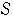
 は右図の斜線部分
は右図の斜線部分 境界線を含む
境界線を含む である.
である.
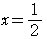
 と線分
と線分 ,
, との交点をそれぞれ
との交点をそれぞれ ,
, とすると,
とすると,
これらの点の座標は,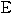
 ,
,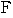
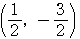
 である.
である.
点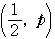
 が領域
が領域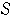
 に属するための条件は,この点が線分
に属するための条件は,この点が線分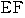
 両端を含む
両端を含む 上にあることである.よって,求める
上にあることである.よって,求める
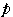
 の値の範囲は,
の値の範囲は,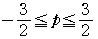
 領域
領域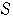
 を表す不等式は,
を表す不等式は,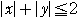
 である.点
である.点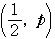
 がこの領域に属するとき
がこの領域に属するとき

 よって,
よって,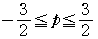
 円
円
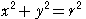
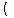
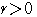
 を円
を円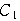
 とする.円
とする.円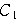
 と正方形
と正方形 の辺および頂点が
の辺および頂点が
 共有点をもつとき,
共有点をもつとき,
ⅰ
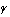
 が最大となるのは,円
が最大となるのは,円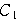
 が正方形に外接するときで,
が正方形に外接するときで,
このときの
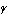
 の値は,
の値は, =
= =
= である.
である.
ⅱ
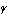
 が最小となるのは,円
が最小となるのは,円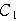
 が正方形に内接するときで,
が正方形に内接するときで,
このときの
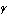
 の値は,中心
の値は,中心 と直線
と直線 との距離に等しい.
との距離に等しい.
ここで,直線 の方程式は,
の方程式は,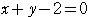
 より,
より,
 =
= =
=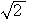
 である.
である.
以上より,求める
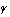
 の値の範囲は,
の値の範囲は,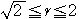
 領域
領域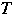
 は直線
は直線
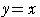
 上の点
上の点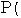
 ,
,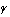
 を中心とし,
を中心とし,
両座標軸に接する円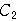
 の周および内部である.
の周および内部である.
中心 が領域
が領域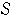
 内にあるとき,すなわち,
内にあるとき,すなわち,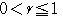
 …①
…①
のときは,明らかに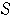
 と
と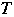
 は共有点をもつ.
は共有点をもつ.
中心 が領域
が領域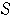
 の外部にあるとき,円
の外部にあるとき,円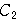
 と線分
と線分 が共有点をもつならば,
が共有点をもつならば,

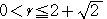
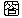
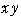
 平面上に4点
平面上に4点 ,
, ,
, ,
, ,
, -
- ,
, ,
, ,-
,- がある.正方形
がある.正方形 の
の
 とする.
とする. 点
点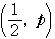
 が領域
が領域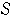
 に属するとき,
に属するとき,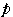
 のとりうる値の範囲を求めよ.
のとりうる値の範囲を求めよ. 円
円
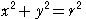
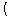
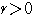
 と正方形
と正方形 の辺および頂点が共有点をもつとき,
の辺および頂点が共有点をもつとき,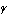
 のとりうる値の範囲を求めよ.
のとりうる値の範囲を求めよ. 不等式
不等式
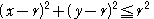
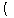
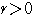
 の表す領域を
の表す領域を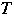
 とする.領域
とする.領域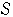
 と領域
と領域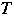
 が
が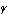
 のとりうる値の範囲を求めよ.
のとりうる値の範囲を求めよ.

 領域
領域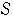
 は右図の斜線部分
は右図の斜線部分 境界線を含む
境界線を含む である.
である.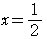
 と線分
と線分 ,
, との交点をそれぞれ
との交点をそれぞれ ,
, とすると,
とすると,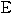
 ,
,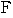
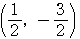
 である.
である.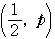
 が領域
が領域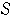
 に属するための条件は,この点が線分
に属するための条件は,この点が線分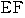
 両端を含む
両端を含む 上にあることである.よって,求める
上にあることである.よって,求める
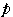
 の値の範囲は,
の値の範囲は,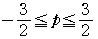
 領域
領域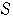
 を表す不等式は,
を表す不等式は,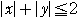
 である.点
である.点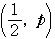
 がこの領域に属するとき
がこの領域に属するとき
 よって,
よって,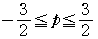
 円
円
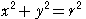
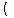
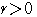
 を円
を円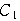
 とする.円
とする.円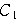
 と正方形
と正方形 の辺および頂点が
の辺および頂点が 共有点をもつとき,
共有点をもつとき,
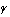
 が最大となるのは,円
が最大となるのは,円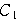
 が正方形に外接するときで,
が正方形に外接するときで,
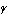
 の値は,
の値は, =
= =
= である.
である.
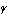
 が最小となるのは,円
が最小となるのは,円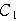
 が正方形に内接するときで,
が正方形に内接するときで,
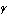
 の値は,中心
の値は,中心 と直線
と直線 との距離に等しい.
との距離に等しい. の方程式は,
の方程式は,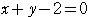
 より,
より, =
= =
=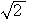
 である.
である.
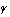
 の値の範囲は,
の値の範囲は,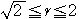
 領域
領域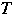
 は直線
は直線
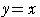
 上の点
上の点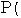
 ,
,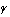
 を中心とし,
を中心とし,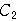
 の周および内部である.
の周および内部である. が領域
が領域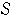
 内にあるとき,すなわち,
内にあるとき,すなわち,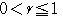
 …①
…①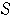
 と
と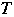
 は共有点をもつ.
は共有点をもつ.
 が領域
が領域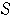
 の外部にあるとき,円
の外部にあるとき,円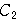
 と線分
と線分 が共有点をもつならば,
が共有点をもつならば,