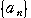
 は等差数列で,
は等差数列で, ,
,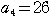
 を満たしている.また,数列
を満たしている.また,数列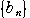
 が
が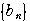
 の初項から第
の初項から第
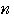
 項までの和を
項までの和を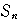
 とすると,
とすると,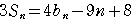
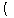
 ,
, ,
, ,…
,… を満たしている.
を満たしている.
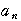
 を
を
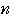
 で表せ.
で表せ.
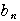
 を
を
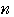
 で表せ.
で表せ.
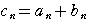
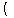
 ,
, ,
, ,…
,… とおくと,すべての自然数
とおくと,すべての自然数
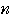
 に対して,
に対して,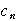
 は9の倍数であることを数学的帰納法で証明せよ.
は9の倍数であることを数学的帰納法で証明せよ.
 等差数列
等差数列 の初項を
の初項を ,公差を
,公差を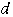
 とおくと,
とおくと,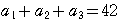
 より,
より, すなわち,
すなわち,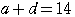
 …①
…①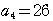
 より,
より,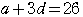
 …② ①,②より,
…② ①,②より, ,
,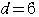
 =
= =
=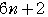
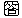

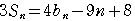
 …③において,
…③において,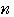
 を
を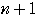
 で置き換えると,
で置き換えると,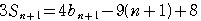
 …④ ④-③より,
…④ ④-③より,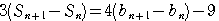
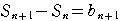
 であるから,
であるから,
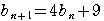
 ここで,数列
ここで,数列 を考えると,
を考えると,
 ,公比
,公比 の等比数列である.③において,
の等比数列である.③において,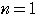
 とおくと,
とおくと,
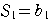
 だから,
だから, よって,初項は
よって,初項は
 =
=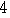

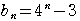
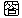

 ,
, の結果より,
の結果より, =
=
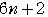
 +
+
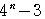
 =
=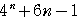

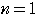
 のとき,
のとき,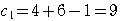
 であるから,
であるから,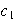
 は9の倍数である.
は9の倍数である.
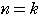
 のとき,
のとき, =
=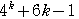
 が9の倍数であると仮定して,
が9の倍数であると仮定して, =
=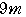

 は整数
は整数 とおくと,
とおくと, =
=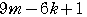
 となるから,
となるから, =
= =
= =
= =
=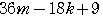

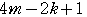
 は整数だから,
は整数だから,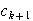
 は9の倍数である.
は9の倍数である. ,ⅱ
,ⅱ より,すべての自然数
より,すべての自然数
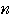
 に対して,
に対して,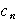
 は9の倍数である.
は9の倍数である.