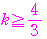:
: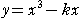
 上の点
上の点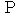
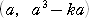
 における接線
における接線
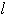
 が,曲線
が,曲線
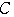
 と点
と点 と異なる
と異なる で交わっている.点
で交わっている.点 における接線が直線
における接線が直線
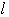
 と直交しているとき,
と直交しているとき, 点
点 の座標を
の座標を
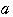
 と
と
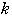
 を用いて表せ.
を用いて表せ.
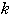
 のとりうる値の範囲を求めよ.
のとりうる値の範囲を求めよ.

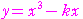
 から
から 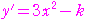
 :
: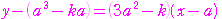
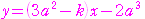
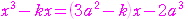
 とすると
とすると 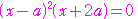


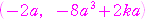
 点
点 における接線の傾きは
における接線の傾きは 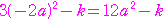
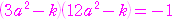
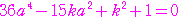


 が存在する条件を求める.
が存在する条件を求める.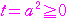
 とおくと
とおくと 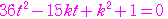
 ……
…… ①
①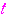
 についての方程式
についての方程式 ①
① が少なくとも
が少なくとも つの負でない
つの負でない の判別式を
の判別式を
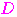
 とすると,実数解をもつことから
とすると,実数解をもつことから 
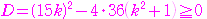
 ,
,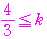
 ……
…… ②
② の
の つの解を
つの解を ,
, とすると,解と係数の関係から
とすると,解と係数の関係から 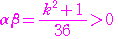
 と
と は同符号であるから,
は同符号であるから, つの正の解をもてばよい.
つの正の解をもてばよい. よって
よって 
 ……
…… ③
③ から
から