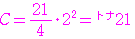から
から までの整数のいずれか一つが書かれたカードが,各数に対して
までの整数のいずれか一つが書かれたカードが,各数に対して 枚ずつ合計
枚ずつ合計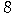
 さんがカードを引いて,賞金を得るゲームをする.その規則は次のとおりで
さんがカードを引いて,賞金を得るゲームをする.その規則は次のとおりで 円のゲーム代を払って,カードを
円のゲーム代を払って,カードを 枚引き,書いてある数が
枚引き,書いてある数が
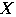
 のとき,
のとき,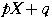
 円
円 ,
,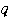
 は正の整数とする.
は正の整数とする. 確率変数
確率変数
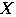
 の平均
の平均 期待値
期待値 は
は
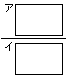
 であり,分散は
であり,分散は
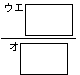
 である.
である.
 さんがカードを
さんがカードを 枚引いて受け取る金額からゲーム代を差し引いた金額を
枚引いて受け取る金額からゲーム代を差し引いた金額を
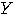
 円と
円と
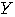
 の平均を
の平均を
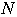
 とするとき,
とするとき,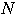
 を
を
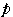
 と
と
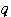
 を用いて表すと
を用いて表すと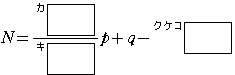
 である.
である.
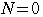
 を満たす
を満たす
 ,
,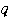
 の値の組の総数は
の値の組の総数は

 である.その中で,
である.その中で,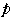
 の最小値は
の最小値は ,最大値は
,最大値は

 である.
である.
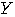
 の分散は
の分散は
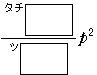
 である.したがって,
である.したがって,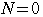
 のとき
のとき
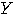
 の分散の最小値
の分散の最小値
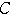
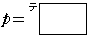
 のとき起こり,
のとき起こり,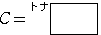
 である.
である.
 確率変数
確率変数
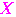
 が,
が, から
から までそれぞれの値をとる確率は,すべて
までそれぞれの値をとる確率は,すべて
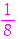
 である
である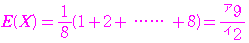
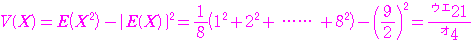


 であるから
であるから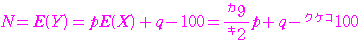

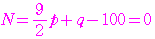
 から
から 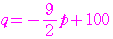

 は正の整数であるから
は正の整数であるから 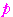
 は偶数 かつ
は偶数 かつ  すなわち
すなわち 
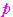
 は正の整数であるから
は正の整数であるから  ,
, ,
, ,……,
,……,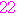
 ,
,
 の組の総数は
の組の総数は
 ,
,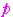
 の最小値は
の最小値は
 ,最大値は
,最大値は

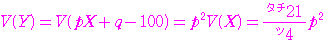
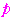
 は正の整数であるから,
は正の整数であるから,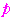
 が最小のとき,
が最小のとき,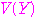
 も最小となる.
も最小となる. から
から
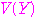
 の最小値
の最小値

 は
は

 のとき起こり
のとき起こり