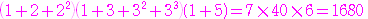,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,……
,…… において
において

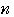
 である項をまとめて,第
である項をまとめて,第
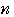
 群とよぶことにする.例えば,第
群とよぶことにする.例えば,第 群は,数列の
群は,数列の 項から始まり,
項から始まり, ,
, ,
, ,
,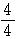
 の
の 項を含んでいる.
項を含んでいる. この数列の第
この数列の第 項は,第
項は,第

 群の中の最初から
群の中の最初から

 番目である.
番目である. 分数を約分した値が
分数を約分した値が になる項が,この数列の中で最初に現れるのは第
になる項が,この数列の中で最初に現れるのは第

 回目に現れるのは第
回目に現れるのは第

 項である.
項である. 第
第 群に含まれる項のうちで,分数を約分した値が整数になる項は
群に含まれる項のうちで,分数を約分した値が整数になる項は

 個
個

 である.
である.
 ア
ア

 イ
イ

 ウ
ウ

 エ
エ

 オ
オ

 カ
カ
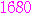
 第
第
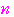
 群には
群には
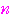
 項含まれている.
項含まれている.
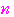
 群の末項は,数列の初項
群の末項は,数列の初項
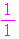
 から数えると
から数えると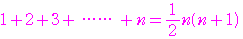
 番目
番目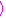
 項が第
項が第
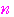
 群にあるとすると
群にあるとすると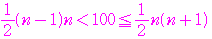
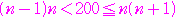
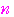
 は自然数であるから,これを満たすのは
は自然数であるから,これを満たすのは
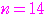
 ,
,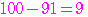
 項は,第
項は,第 群の中の最初から
群の中の最初から 番目.
番目.
 が最初に現れるのは,第
が最初に現れるのは,第 群の初項であるから,
群の初項であるから,
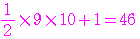
 番目
番目 である.
である. 回目に表れるのは
回目に表れるのは
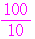
 のときであるから,
のときであるから, 群の
群の 番目となり,
番目となり,
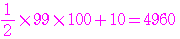
 番目
番目 である.
である. 第
第 群の
群の
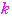
 番目
番目 ただし
ただし
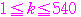
 は
は
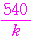
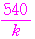
 が整数となるのは,
が整数となるのは,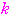
 が
が
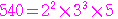
 の正の約数のときである.
の正の約数のときである.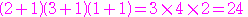
 個
個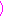
 の正の約数の総和と一致する.
の正の約数の総和と一致する.