 の辺
の辺 の中点を
の中点を ,線分
,線分 の中点を
の中点を ,線分
,線分 の中点を
の中点を とす
とす と平面
と平面 の交点を
の交点を とする.
とする. ,
, ,
, として
として
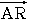
 を
を
 ,
, ,
,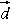
 で表せ.
で表せ. 
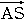
 を
を
 ,
,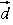
 で表せ.
で表せ. 直線
直線 と
と の交点を
の交点を とするとき,
とするとき,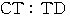
 を求めよ.
を求めよ.

 …
… ①
① は平面
は平面 上にあるから,実数
上にあるから,実数
 ,
, を用いて,
を用いて, …
… ② と表される.
② と表される. 点
点 ,
, ,
, ,
, は同じ平面上にないから,①,②
は同じ平面上にないから,①,② より
より ,
,
 ,
,
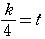
 ,
,
 ,
,
 よって,
よって,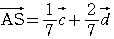
 点
点 は直線
は直線 上にあるから,
上にあるから,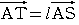
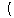
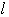
 は実数
は実数 とおける.
とおける. から
から 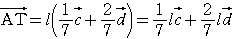
 は直線
は直線 上の点であるから
上の点であるから  ゆえに
ゆえに 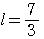
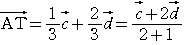
 は辺
は辺 を
を :
: の比に内分する点である.
の比に内分する点である.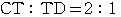
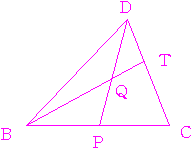
 底面の△
底面の△ にメネラウスの定理を使うと,
にメネラウスの定理を使うと,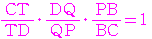
 となるから,
となるから, :
: =
= :
:
 とおくと,
とおくと,

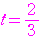
 :
: =
= :
:
 先に
先に から求まってしまうが…
から求まってしまうが…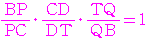
 となるから,
となるから, :
: =
= :
: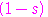
 とおくと,
とおくと,

 よって,
よって, :
: =
= :
: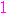
 にメネラウスの定理を使うと,
にメネラウスの定理を使うと,
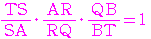
 となるから,
となるから, :
: =
= :
: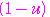
 とおくと,
とおくと,

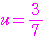
 :
: =
= :
: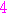
 =
= =
= =
=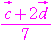
 =
= =
= =
= =
=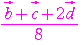
 となる.
となる.