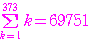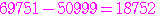,
, ,
, ,……
,…… から
から の倍数,
の倍数, の倍数,
の倍数, の倍数を取り除いて得られる
の倍数を取り除いて得られる ,
, ,
, ,……
,…… について,次のものを求めよ.
について,次のものを求めよ.
 以下の数の個数
以下の数の個数  第
第 項
項  初項から
初項から 項までの和
項までの和

 以下の自然数の中に,
以下の自然数の中に, の倍数は
の倍数は 個,
個, の倍数は
の倍数は 個,
個, の倍数は
の倍数は 個,
個, の倍数は
の倍数は 個,
個, の倍数は
の倍数は 個,
個, の倍数は
の倍数は 個,
個, の倍数は
の倍数は 個ある.
個ある. ,
, ,
, の少なくとも
の少なくとも つで割り切れる数の個数は
つで割り切れる数の個数は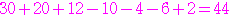
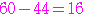
 個
個

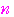
 を自然数とすると,
を自然数とすると, から題意の数列の
から題意の数列の
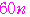
 以下の数の個数は
以下の数の個数は
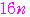
 個で
個で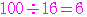
 余り
余り であり,
であり, ,
,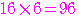
 であるから,
であるから, 項までは
項までは 以下にある.また,
以下にある.また, は題意の数列の項であるから,
は題意の数列の項であるから, から
から 番目の項が第
番目の項が第 項である.
項である. ,
, ,
, ,
, ,……
,…… 項は
項は 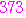

 から,
から, 以下の自然数について考える.
以下の自然数について考える. 以下の自然数の中に,
以下の自然数の中に, の倍数は
の倍数は 個,
個,  の倍数は
の倍数は 個,
個,  の倍数は
の倍数は 個,
個, の倍数は
の倍数は 個,
個,  の倍数は
の倍数は 個,
個,  の倍数は
の倍数は 個,
個, の倍数は
の倍数は 個
個 ,
, ,
, の少なくとも
の少なくとも つで割り切れる数の総和は
つで割り切れる数の総和は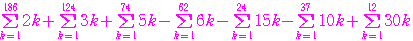

 以下の自然数の総和は
以下の自然数の総和は