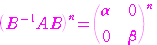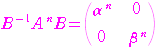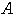
 に対し,逆行列をもつ行列
に対し,逆行列をもつ行列
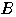
 を見つけて,
を見つけて,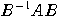
 の
の
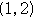
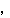
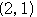
 成分を
成分を にす
にす
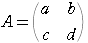
 に対して,方程式
に対して,方程式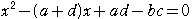

 を対角化してみよう.このとき,上記の方程式
を対角化してみよう.このとき,上記の方程式
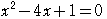
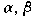
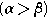
 とし,次の行列
とし,次の行列
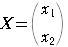
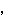
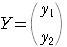
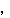
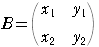
 を考える.
を考える.
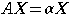
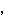
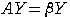
 を満たす
を満たす

 でない
でない
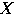
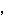
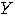
 をそれぞれひとつずつ求めよ.
をそれぞれひとつずつ求めよ.
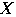
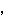
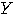
 に対し,
に対し,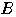
 が決まる.
が決まる.
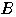
 の逆行列を求め,
の逆行列を求め,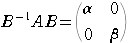
 を示せ.
を示せ. 行列
行列
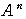
 の各成分を
の各成分を の式で表せ.ただし,
の式で表せ.ただし,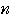
 は自然数とする.
は自然数とする.
 方程式
方程式
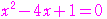
 の解が,
の解が,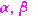

 であるから
であるから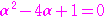
 …
… ①
①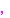
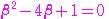
 …
… ② :この
② :この ,
, を固有値という.
を固有値という.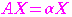
 から
から 
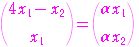
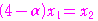
 ……
…… ③
③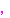
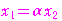
 ……
…… ④
④ より,
より,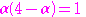
 であるから
であるから  :
: :
:
 ④
④ は同値であるから,③
は同値であるから,③ ④
④ を満たす
を満たす
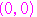
 以外の解の
以外の解の つは
つは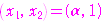
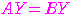
 から
から
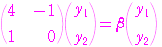
 を満たす
を満たす
 以外の解の
以外の解の つは
つは したがって
したがって 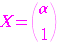
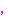
 :この
:この ,
, を固有ベクトルという
を固有ベクトルという
 ,
, であるから
であるから 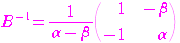
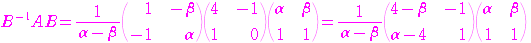


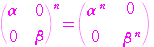
 ……
…… ⑤
⑤ が成り立つと仮定すると
が成り立つと仮定すると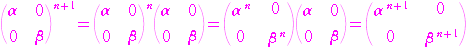
 となる.
となる.
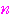
 に対して,⑤
に対して,⑤ が成り立つ.
が成り立つ.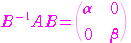
 から
から